Encompasses Positron Emission Tomography (PET), Sctintigrapy/Gamma cameras, and Single Photon Emission Computed Tomography (SPECT), as well as certain therapeutic treatments.

Nuclear medicine involves the injection, ingestion, or inhalation of a radioactive substance called a radiotracer, radiopharmaceutical, or radioactive drug. These are molecules with a radioactive isotope attached.

For therapy, radioactive isotopes emit beta (electrons) or alpha (helium nuclei) particles that only travel a short distance (millimeters) within the patient. The radioactive isotopes are attached to drugs that go into cancer cells. The isotopes deposit energy, which then leads to the death of the nearby cancer cells. Thyroid treated using Iodine-131 and prostate cancer treated using Lu-177 PSMA are two common uses of therapeutic radiopharmaceuticals.

For imaging, the radioactive isotopes attached to the molecules emit photons that pass through the patient and can be detected and used to generate images. Depending on the type of molecule used, where it goes can tell us how the body is functioning. The most common usage in PET imaging is to detect cancer and metastasis. Many cancers are growing and use a lot of sugar. A radioactive isotope attached to a glucose-like molecule will go preferentially to tumors and imaging the emitted photons can then show us where those tumors are in the body.

Radioactivity

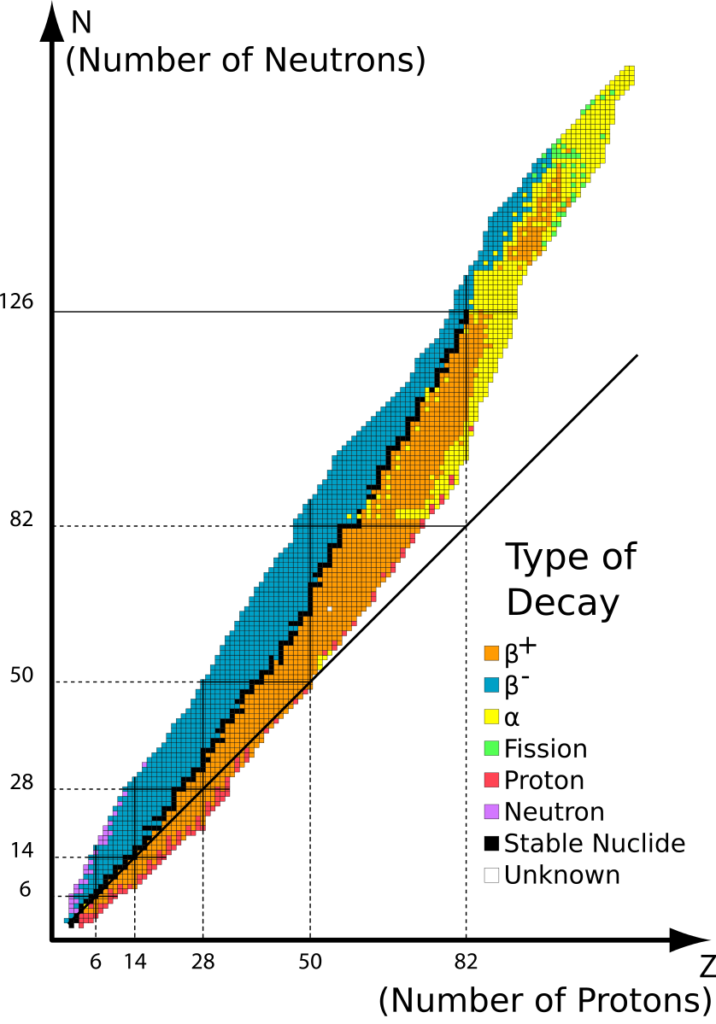
Some isotopes of elements are unstable. They usually have too many protons or too many neutrons.

β+ decay and electron capture happen when there are too many protons

Nucleus converts proton to neutron (or captures an orbital electron), emits β+ (and a neutrino)

β– decay happens when there are too many neutrons

Nucleus converts neutron to proton, emits β- (and a antineutrino)

α decay happens for the heavier elements

Nucleus splits and emits a helium nucleus (2p2n)

Half-life, T_1/2

Radioactive isotopes are characterized not just by their emitted particles but also by their half-lives. That is the time is takes for half of a sample of the isotopes to decay away. The decay is exponential given by the equation

A = −dN/dt = λN –> A(t)=A₀e^−λt

where A is the activity, λ = ln(2)/T_1/2 = decay constant, and N is the number of isotopes. The activity, or rate of change in the number of radioactive atoms, is proportional to the current number of atoms.

In medical imaging we want to use isotopes with half-lives similar to the biological half-life of the molecule they are attached to. Most radiotracers have half-lives between 1-6 hours (with some exceptions). If the half-life is too short, they will all decay before the molecule gets to where it is going. If it is too long, then it takes longer to collect enough photons for an image and increases the radiation dose to the patient.